Introduction to Systems Thinking
People, when initially introduced to structures, also referred
to as Archetypes, often find them a bit overwhelming. They really
aren't at all difficult once you get used to them. The following
is an introduction to structures and how to read the stories associated
with the diagrams.
The basic idea of structure(s) is to point out the influence
one thing has on another. That is, how do things influence other
things to change.
If I have two things, thing 1 and thing 2, there
are only two ways thing1 can influence thing2.

Figure 1: Add Relationship
As indicated in Figure 1, thing 1 can add to thing
2, as indicated by a "+" sign, thus increasing thing
2.
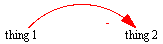
Figure 2: Subtract Relationship
The alternative is that thing 1 can subtract from thing
2, as indicated by the "-" sign in Figure 2, thus
decreasing thing 2.
All this thingness may a bit difficult to connect with so let's
consider a couple specific examples.

Figure 3: Sales Increases Revenue
Figure 3 indicates that sales adds to revenue.
Even if sales decrease it will still add to revenue,
just not quite as rapidly as before. On the other hand, if sales
increases it will add even more readily to revenue.

Figure 4: Product Sales and Inventory
Figure 4 indicates that product sales subtracts from
finished goods inventory. If product sales increase
it will subtract even more from finished goods inventory.
On the other hand, if product sales decrease it will still
subtract from finished goods inventory, just not quite
so much.
Within systems diagrams there are often items that are held
constant within the context of what is being considered. These
items will have neither a "+" nor a "-" attached
to them.
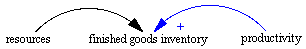
Figure 5: Constant Contribution
Figure 5 indicates that resources interact with productivity
in such as way as to add to the finished goods inventory.
The indication is that resources is a constant within the
structure being considered so it neither adds to nor subtracts
from, it just is. You might think of a constant as a catalyst
for the result. If productivity increases it will interact
with resources and add even more to finished goods inventory.
If productivity decreases it will still interact with resources
to add to finished goods inventory, just not so readily.
Now that we've covered connections, let's cover connections
that complete to form loops. There are only two types of loops,
reinforcing and balancing.
Reinforcing Loop
A reinforcing loop is one in which the interactions are such
that each action adds to the other. Any situation where action
produces a result which promotes more of the same action is representative
of a reinforcing loop.

Figure 6: Reinforcing Loop
Figure 6 indicates what happens in a typical savings account.
The principal in the savings account interacts with the
interest rate and adds to the interest. Note that
interest rate is considered to be a constant in this example.
Interest then adds to the principal. This reinforcing
action happens every so many months depending on the period over
which the institution computes the interest. The snowball
rolling down hill is your signal that the loop is a reinforcing
loop. The small graph to the right of principle indicates
that the growth of principal is exponential.
Typical examples of reinforcing loops are population growth
and decline, uncontrolled nuclear reactions, snow balls rolling
down hill of course, runs on banks, wall street market crashes,
etc.
Balancing Loop
A balancing loop is one in which action attempts to bring two
things to agreement. Any situation where one attempts to solve
a problem or achieve a goal or objective is representative of
a balancing loop.
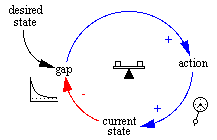
Figure 7: Balancing Loop
Figure 7 provides the basic form of the balancing loop. The
desired state interacts with the current state to
produce a gap. The gap adds to the action
and the action adds to the current state. The current
state then subtracts from the gap. The small clock
to the right of the arc between action and current state
indicates some time delay that it takes for the action
to change the current state. As the current state
gets closer to the desired state the gap gets smaller
and smaller so it adds less and less to the action, which
is adding to the current state. Once the action
has moved the current state to a point where it equals
the desired state the gap is zero and there's no
more addition to the action, so there is no more action.
The balance in the center of the loop is your indication that
the loop is a balancing loop.
Typical examples of balancing loops are driving from location
A to location B, developing a skill, building something, fixing
a problem, etc.
Telling one Loop from Another
Initially you might consider it difficult to figure out one
loop from the other, yet it's simply a matter of counting. All
you need to do is count the number of minus signs around the loop.
If there is an even number, or zero, minus signs then it is a
reinforcing loop. If there is an odd number of minus signs then
it's a balancing loop.
These two loops can combine in numerous ways resulting in typical
situation characteristics we recognize in our daily lives. theWay of Systems matches situation
descriptions to common combinations of reinforcing and balancing
loops which have very distinct characteristics.
Now that wasn't so tough, was it? You may have been expecting
there was more to it than this, yet there really isn't. When one
thing affects another thing it can only add to or subtract from
that which it affects, otherwise there would be no influence at
all now would there.
Systems Thinking: An Operational
Perspective of the Universe provides a more elaborate background
than this initial introduction though theWay
of Systems presents a more integrated view of the archetypes.
Also, George Richardson's "Problems
with causal-loop diagrams" is a marvelous read.
theWay of Systems
* Feedback
* Musings
Copyright © 2004 Gene Bellinger
|